1. Inverting Redshift
Redshift (z) can be quantified by comparing the observed energy (Eobs) of a photon to its original energy (Eemit):
If the photon is observed to have less energy than when it was emitted (Eobs < Eemit), then z > 0 and the photon is redshifted. When the photon gains energy (Eobs > Eemit), then z < 0 and the photon is blueshifted. Since the photon will always have a positive energy, Eemit / Eobs is always greater than zero, so z is always greater than -1. Thus, the range of redshifts is infinite (z > 0), and the range of blueshifts is finite (-1 < z < 0).
As an alternative, consider what happens when equation (1) is inverted and set equal to 1 + b:
When b > 0, that means the photon has gained energy, which is blueshift. When b < 0, the photon has less energy than when it was emitted, so the photon is redshifted. Since the photon's energy will never be negative or zero, b is always greater than -1. Quantified this way, the range of redshifts is finite (-1 < b < 0).
The range of redshifts can be either infinite (as z) or finite (as -b):
|
z > 0 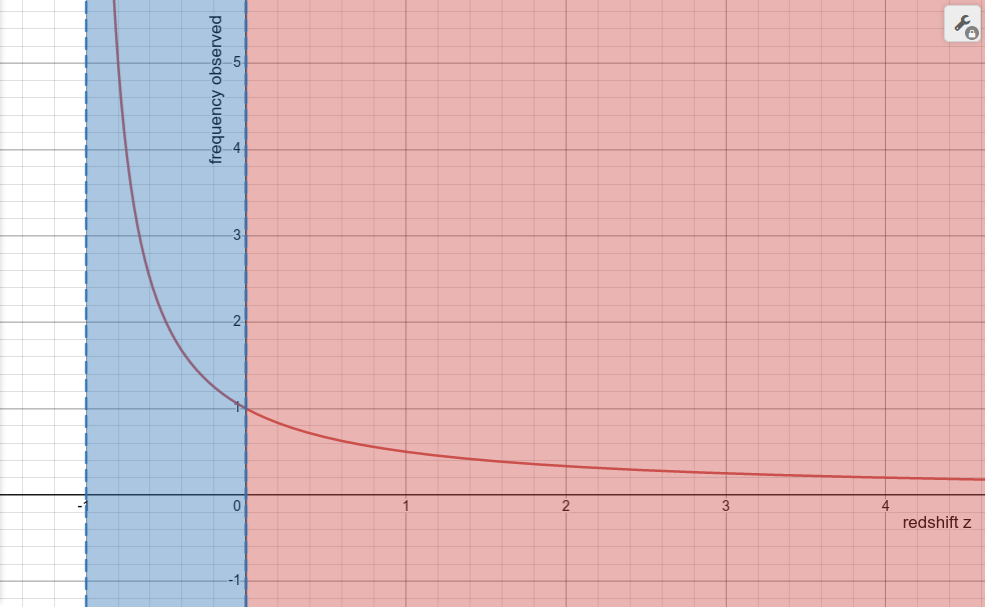 |
-1 < b < 0 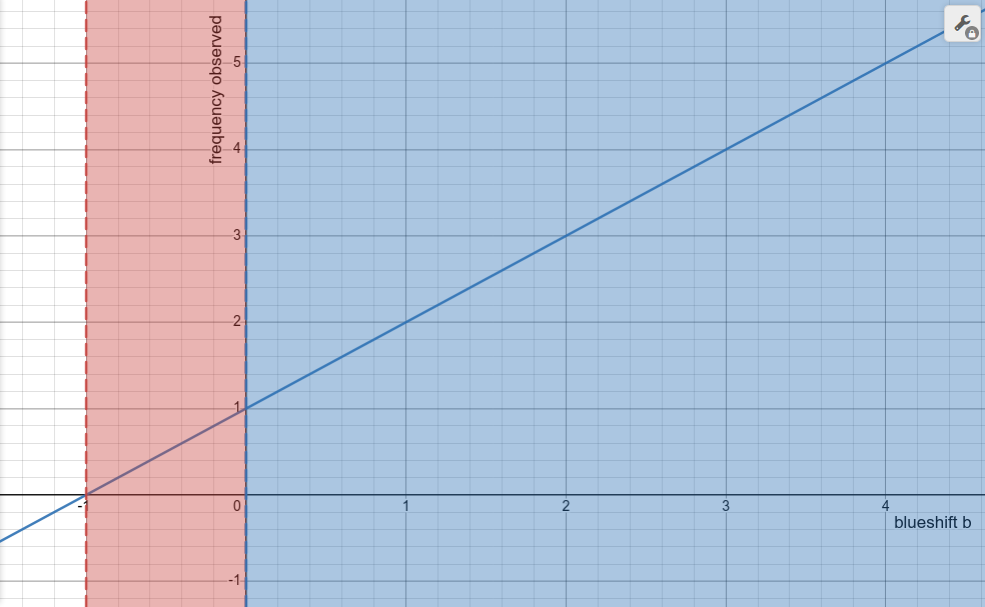 |
2. Distance
The traditional redshift-distance relationship is:Where d is distance, c is the speed of light, and H0 is Hubble's constant. This equation is an approximation that is only valid for very small redshifts (z ≪ 1).
Substituting z with the alternative quantification, -b:
Solving equation (2) for b and simplifying:
Substituting (5) into (4) gives the alternative redshift-distance relationship:
Comparing the two distance relationships (Fig. 1) shows that the distance predicted by the traditional equation climbs to infinity while the alternative equation converges on c / H0. This is due to the range of redshifts being infinite as z and finite as -b (i.e. z / (1 + z)).
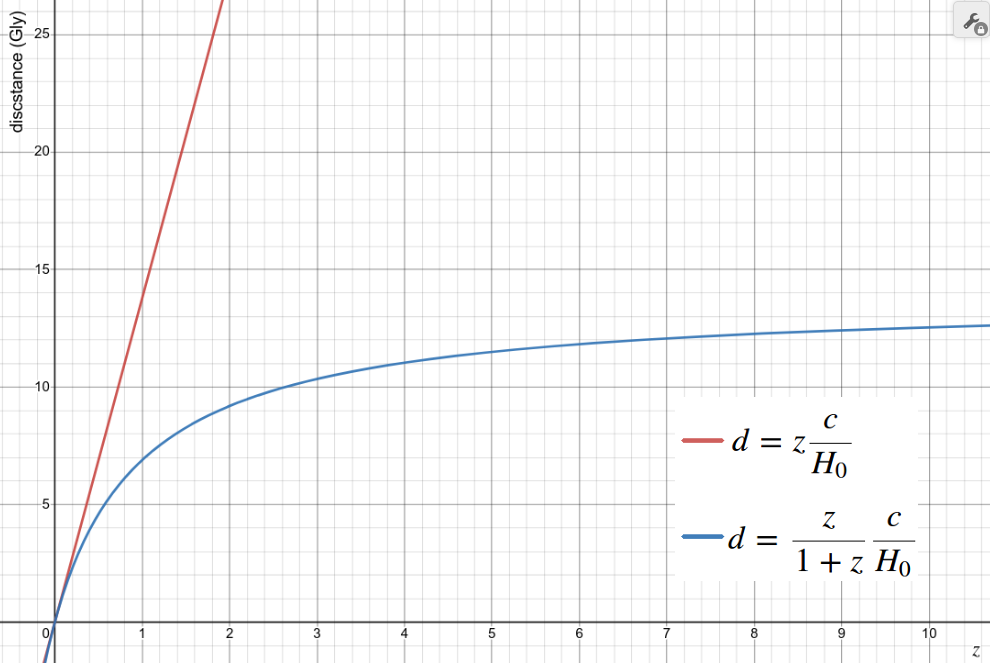
Figure 1. The traditional and alternative redshift-distance relationships.
3. Lookback Time
Dividing both sides of equation (6) by the speed of light, c, gives the alternative redshift-time equation:
This equation is also the solution to the lookback time integral for what's known as an "empty" Friedmann-Lemaître-Robertson-Walker (FLRW) model.[1]
In Fig. 2, the alternative redshift-time equation is compared to the lookback times of three FLRW models: an empty model (ΩM=0, Ωλ=0), a matter-only model (ΩM=1, Ωλ=0), and the concordance model, (ΩM=0.32, Ωλ=0.68).

Figure 2. The redshift-time relationships compared to FLRW lookback times.
The empty model and the concordance model have similar predictions while the matter-only model predicts a far younger universe. The lookback times predicted by the empty FLRW model are identical to the times given by the alternative redshift-time equation.
4. Conclusion
When quantified as z the range of redshifts is infinite. When quantified as -b, however, the range is finite. The traditional and alternative quantifications of redshift lead to two distance relationships. The traditional relationship is linear, and only a valid approximation for very small values of z. The alternative relationship is identical to an empty FLRW model, and a reasonable approximation to the concordance model.
While the choice between quantifications of redshifts initially seems arbitrary and inconsequential, upon further investigation, the inverted, alternative quantification is a more accurate representation of the universe.