Hubble's Law and Cosmic Time Dilation

The familiar interpretation of red-shifts as velocity-shifts very seriously restricts not only the time scale, the age of the universe, but the spatial dimensions as well. On the other hand, the alternative possible interpretation, that red-shifts are not velocity-shifts, avoids both difficulties, and presents the observable region as an insignificant sample of a universe that extends indefinitely in space and in time.

Edwin Hubble, The Observational Approach to Cosmology, pg. 47, 1937

Videos:

• YouTube channel: Nonexpanding

Tools:

• Supernovae data and model visualization - supernovae.htm
• Curve fitting the Supernovae data with squared sum of errors (SSE) - sse.htm
• Visual FLRW/ΛCDM graphing calculator - flrw.htm
• Volume divider for making galaxy count predictions - volume.htm

Observation

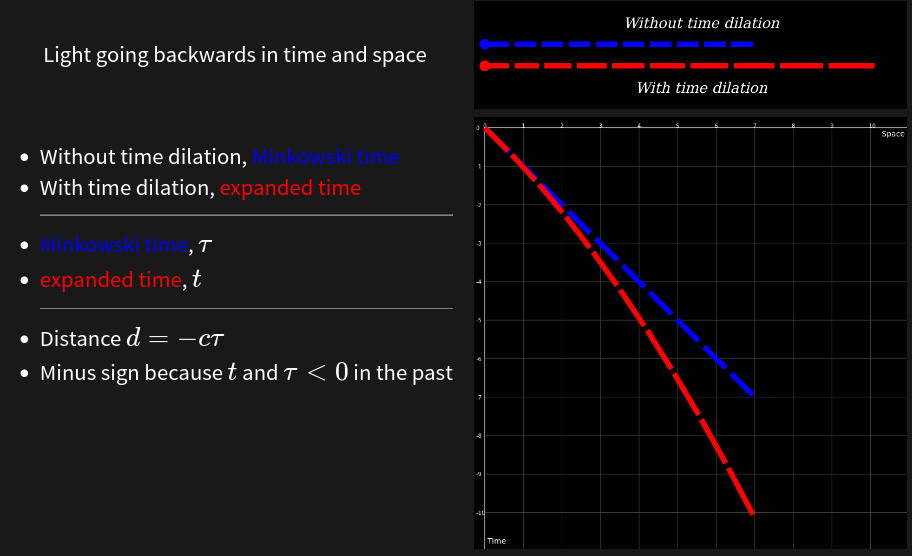
We observe cosmological redshift and cosmic time dilation. These are interpreted as effects of the expanding universe. Light stretched in space would get a longer, redder, wavelength.

Light would also be redshifted were the wave's period to increase somehow. Since the observed duration of a distant supernovae is stretched, then it would follow that the duration of all similarly distant phenomena would be equally stretched, including the oscillations of electromagnetic waves emitted from that distance.

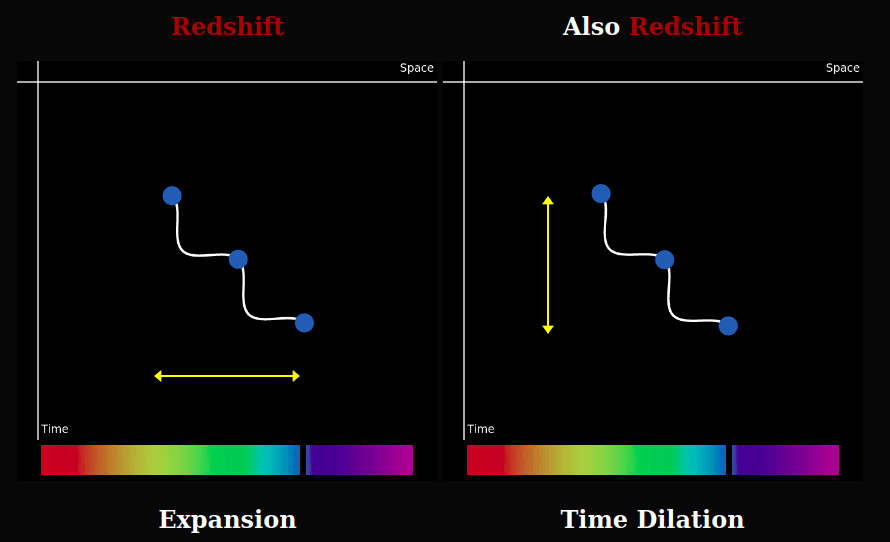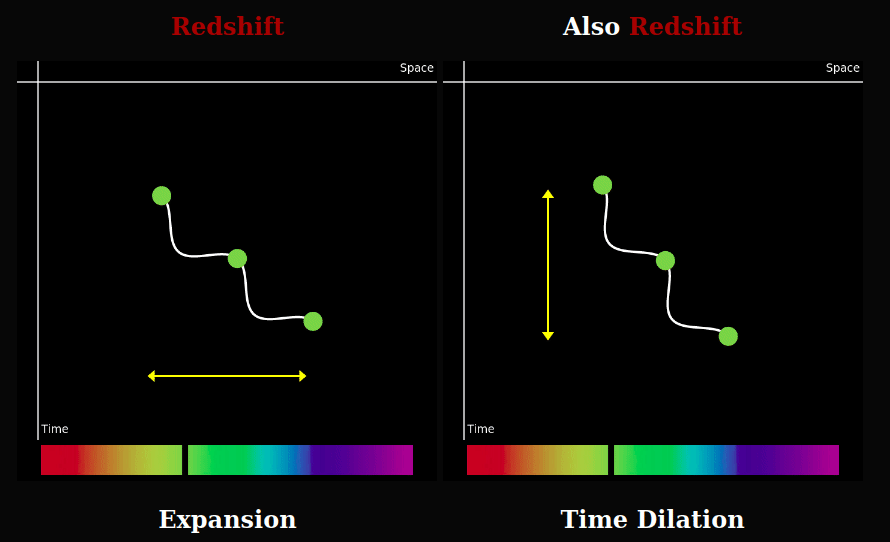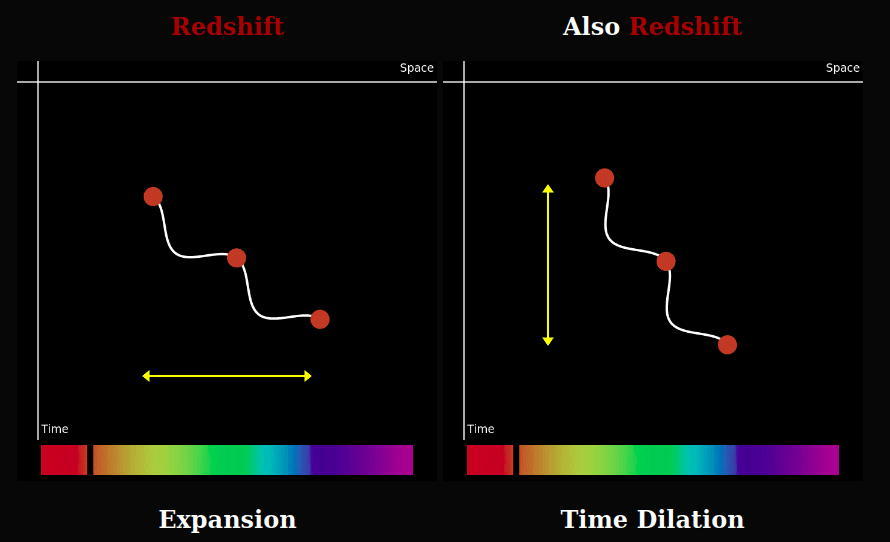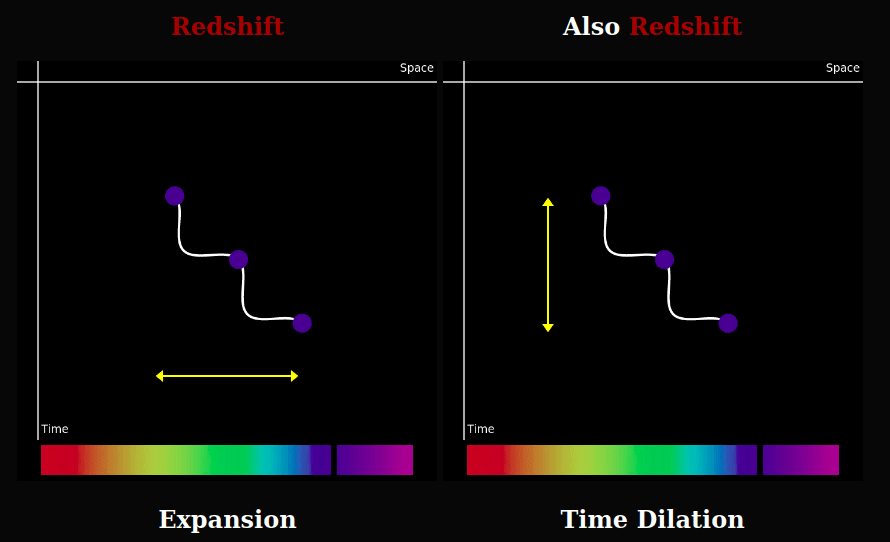
Conjecture

Consider the possibility that the time dilation we observe is actually what's happening. It's not an illusion caused by something else. What we see is real. Perhaps time itself is speeding up, so the clocks in the present are running faster than they were in the past. This makes an expanding universe, and thus a big bang, inflation, and dark energy unnecessary.

The conjecture can be summarized as "the past is time dilated".

Hypothesis

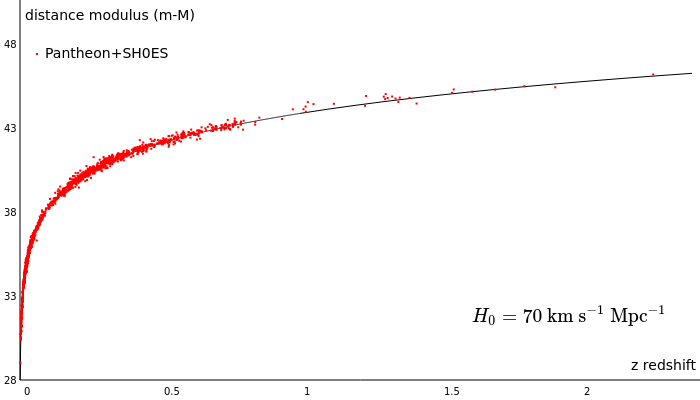
Compared to data

The hypothesis against the Pantheon+SH0ES dataset.

mike@mikehelland.com